今回のコラムでは、資産形成において非常に重要な概念である「複利の力」についておご説明します。
複利とは何か、その具体的な活用方法、そして将来の資産形成にどれほど影響を与えるかについて詳しく解説していきます。
「複利」とは?
複利とは、元本に対して利息がつくだけでなく、その利息にもさらに利息がつく仕組みのことを指します。
つまり、利息が利息を生むということです。
この仕組みが長期にわたって働くことで、元本が大きく増加する効果をもたらします。
たとえば、100万円を年利2%で運用した場合、1年後には102万円になります。この2万円の利息は次の年には元本と合わせて104万400円になり、その次の年には106万1208円となります。
このように、利息が元本に加わり、さらにその利息が新たな元本となって利息を生むことで、資産は指数関数的に増加していきます。
複利を理解するための3つの係数
複利を効果的に理解し活用するためには、次の3つの係数について知っておくことが重要です。
以下に、各係数における年利1%から10%までの範囲での増え方を表にして掲載します。
年利が大きくなるほど増え方が急激になることに注目してください。これこそが複利のインパクトです。
1.終価係数
終価係数とは、一定の元本を特定の利回りで運用した場合、将来どのくらいの価値になるかを示すものです。
- 手元資産を一定の利回りで運用すると、将来いくらになるか
- モノやサービスの値段が一定の率で上昇すると、将来いくらになるか
- 現在100 万円のモノやサービスが年2%(複利)で上昇すると、20年後はいくらになる?
- 100万円 × 1.49 = 149万円になる
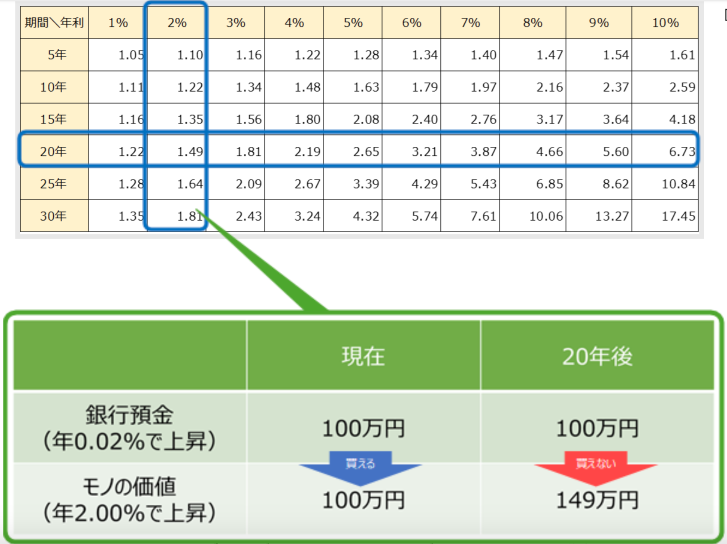
つまり、100万円で買えたはずのモノが149万円を出さなければ買えなくなるのです。
物価上昇をしているときに100万円を銀行に預け入れているだけでは、そのお金に実質的な目減りが起こるという「インフレリスク」を保有しています。
インフレリスクをカバーするためには、収益性が⾼いリスク商品にも⽬を向ける必要があり、終価係数はおおよその目標を立てるときに活用できます。
2.年金終価係数
年金終価係数は、毎年一定額を積み立てた場合に、将来どのくらいの資産になるかを示すものです。
- NISAのつみたて投資枠の限界(1,800万円)まで積み立てた場合、15年後にはいくらになる?
(毎年120万円ずつ積み立て、年6%(年複利)で運用) - 120万円 × 23.28 = 約2,794万円になる(+994万円)
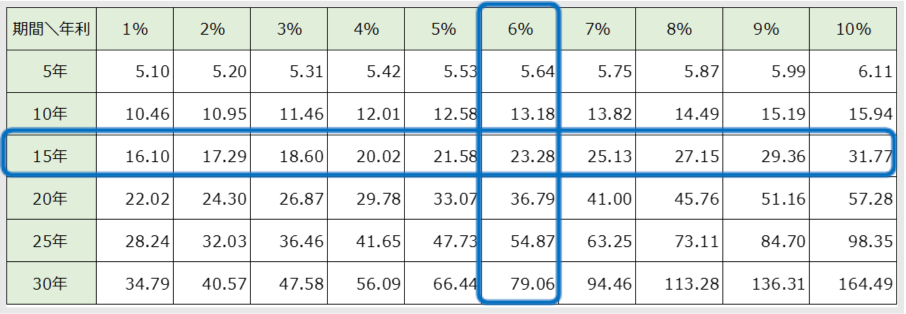
投資累計額は1,800万円でしたが、運用によって994万円も増えています。
現在投資に悩む45歳の方でも、60歳まで積み立てて運用すれば2,794万円まで増やせる可能性があることを意味します。
3.資本回収係数
資本回収係数は、一定期間にわたって毎年定額を取り崩す場合、毎年いくら受け取れるかを示すものです。
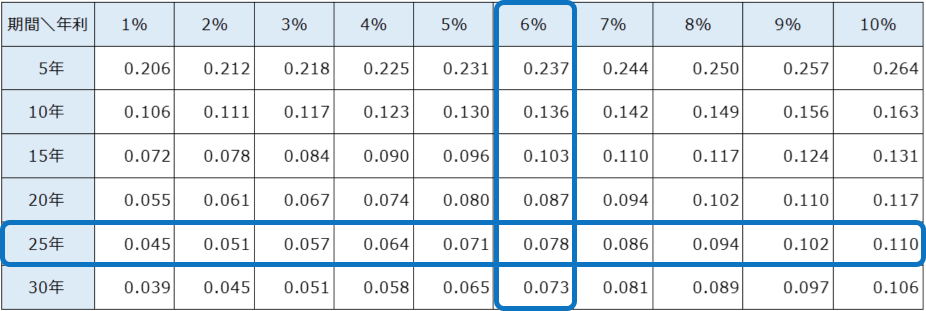
- NISAで運用しながら一定金額を取り崩すとき、毎年いくらずつ受け取れる?
(年6%(年複利)で運用し、25年間 にわたって毎年定額を取り崩す場合) - 2,794万円 × 0.078= 毎年218万円ずつ受け取れる(+ 2,656万円)
上記のような方法で取り崩しても、資産は2,656万円も増加しています。
つまり、複利の力を利用すると、現役時代よりも引退後の方が資産がより増えるということが起こり得るのです。
複利のインパクト
表1~ 表3を見て分かるように、それぞれの係数は表の右下に行くほど高くなります。
つまり、高い年利と期間を長く取るほど、複利効果が等比級数的に高くなっていきます。
資産運用において、高い利回りばかりを狙うとリスクが高まるので考慮が必要ですが、長期性の確保が前提であることは間違いありません。
また、忘れて欲しくないのは複利の効果が運用だけでなく、物価上昇にも影響する点です。
物価が上昇すると、その影響は複利で効いてくるため、インフレリスクを意識しなければ生活が困難になります。物価上昇率が高くなると、終価係数表(表1)の右側にシフトすることによって、将来のモノの値段が急激に高まることを理解し、適切な対策を取ることが重要です。
まとめ
複利の計算を理解するのは難しくありませんが、実際に活用するためには、将来のどの分野に対してどれほどのインパクトで影響を与えるのかを知る必要があります。
その意味で、①終価係数、②年金終価係数、③資本回収係数による将来への影響を考える習慣を持ってみましょう。
この習慣が、複利の力を最大限に活用し、将来の安定した生活を実現することにつながります。


